Comptar amb el zero

Quan Pedro Sánchez va anunciar les famoses fases de la desescalada va provocar un petit embolic, moltes vegades en sentit jocós, amb el fet que fossin quatre fases però numerades des de la zero a la tres. Aquesta confusió es produeix perquè es comença a comptar pel zero enlloc de començar per l’u, que és tal com es fa habitualment. Però té sentit començar a comptar pel zero enlloc de l’u? Serveix per a comptar el número zero?

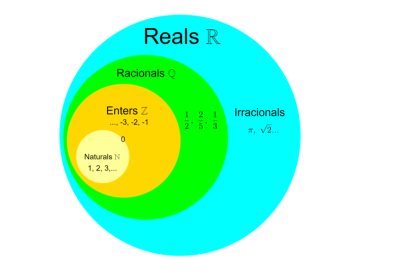
Quan l’ésser humà va començar l’activitat matemàtica de comptar no comptava fases sinó que tenia la necessitat de comptar fruites o bisons pasturant. La primera part del procés va ser agrupar objectes uniformes, és a dir allò que en matemàtiques sempre diem de no barrejar peres amb mançanes. La segona fase fou aparellar els objectes agrupats, d’aquí que hi hagi moltes teories que afirmen que el primer número que va existir va ser el dos, perquè si només hi havia una sola cosa l’Homo Habilis no tenia cap necessitat de comptar res. I a partir d’aquí ja es van començar a agrupar de tres en tres o de quatre en quatre i va venir la tasca de crear paraules per a designar els números i més endavant d’escriure’ls. Aquests nombres 1, 2, 3, 4, 5... s’anomenen nombres naturals.

Els egipcis, cap a l’any 2000 aC, tenien maldecaps una mica més complicats que els de l’home prehistòric com el fet de repartir dos pans entre cinc persones. Amb problemes com aquest i molts més trobats en els papirs Rhind i de Moscou, els egipcis van tenir la necessitat de començar a treballar amb fraccions: 2/5, 1/4, 1/3 … evidentment no les escrivien amb aquesta notació sinó amb la seua simbologia. Aquests números fraccionaris poden expressar-se en forma de nombre decimal exacte 0,4, 0,25 o periòdic 0,333333, tal com va generalitzar Simon Stevin al segle XVII.

Els grecs, al segle V, van descobrir que, a part dels nombres naturals i dels fraccionaris, n’existien uns altres que van provocar el caos: els nombres irracionals. Aquests nombres amb infinits decimals sense període que no els entraven al cap van ocasionar el suïcidi d’alguns pitagòrics. Són nombres irracionals el conegut nombre Pi (π) o l’arrel quadrada de 2.

Els negatius van arribar tard, quan van ser necessaris en comptabilitat o per marcar referències geomètriques: positiu cap amunt i negatiu cap avall, com en els pàrquings. Així en ajuntar els naturals 1, 2, 3… i els seus negatius -1, -2, -3,... obtenim l’anomenat conjunt dels nombres enters. Si a aquests enters hi afegim les fraccions, obtenim el conjunt dels nombres racionals. I si als racionals hi afegim els nombres irracionals, es forma el conjunt dels nombres reals.

Però, i el zero? Ens hi cap, al conjunt dels naturals? O l’hem d’afegir als enters com a element de separació dels positius amb els negatius? Hem vist que els nombres naturals serveixen per comptar i ordenar, però el zero? L’ús del zero com a número es deu a les matemàtiques índies cap allà el 650 dC, Fibonacci el va introduir a la matemàtica europea al segle XIII però no s’hi va mullar gaire. Durant el segle XX matemàtics com Dedekind, Hilbert, Cantor i Peano van formalitzar matemàticament els conjunts de nombres i s’optà per classificar el zero com a nombre enter i no com a natural.

Una reflexió Però té sentit comptar zero coses? Avui en dia els matemàtics encara no es posen d’acord. Personalment penso que no té sentit comptar alguna cosa com a zero, perquè en si ja és alguna cosa. Per tant anomenar zero la primera fase és contradictori en essència. Si és la primera fase no pot ser zero, és un. El zero no hauria de ser natural, però ho deixo a gust del lector