A un quilòmetre de casa

Ja fa uns dies,

l’anomenada

autoridad competente

, dins de les restriccions de la fase 0 –també té la seua cosa començar a comptar des del zero i no des de l’1– del pla de desescalada enfront del Covid-19 se’ns deia que podríem passejar dins de les franges horàries corresponents fins a una distància d’un quilòmetre de casa nostra.

A l’hora de calcular aquesta distància el més senzill seria pensar en una circumferència de radi d’1 km amb centre justament a casa nostra i això ens donaria tot el conjunt de punts que es troben a distància d’1 km. Però realment caminaríem 1 km per arribar a aquests punts de la circumferència que estan a 1 km en línia recta de casa nostra? En una geometria plana –nosaltres vivim en una d’esfèrica, però en distàncies curtes la podem aproximar per una de plana– la distància més curta entre dos punts és la línia recta, però això a les ciutats no passa. Normalment no podem caminar en línia recta per anar entre un punt i un altre, més que res perquè ens trobem edificis pel mig i no tenim la propietat de traspassar-los com si fóssim fantasmes.

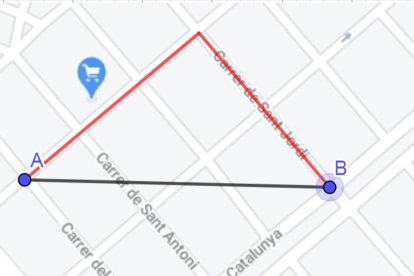
Per simplificar-ho podem imaginar-nos els carrers com una quadrícula: el barri de l’Eixample de Barcelona o el districte de Manhattan de Nova York ens van molt bé i a Lleida podem pensar en la zona vora del Rectorat de la UdL o en el nucli urbà d’Almacelles, que és el tros de plànol de la imatge. Per anar d’un punt A a un B ens fixem que no podem anar en línia recta sinó que ens hem de moure en ziga-zagues rectangulars de tal manera que el recorregut és un múltiple de trams horitzontals i verticals. Si construïm un triangle rectangle veiem que la distància serà la suma de les longituds dels catets, que és major que el valor de la hipotenusa, distància recta entre A i B. Per tant, si preneu un punt que a una distància recta estigui a 1 km realment caminareu més d’1 km. A aquest càlcul de distàncies se l’anomena mètrica Manhattan.

Una altra cosa que podem calcular és el nombre d’itineraris diferents que es poden fer per anar des del punt A al B, perquè podem passar per diferents carrers. Matemàticament és un problema de combinatòria amb moviments verticals i moviments horitzontals. Primer definim el factorial d’un nombre

n

que se simbolitza

n!

i és el resultat de la multiplicació d’un número natural pels seus anteriors fins a l’1. Per exemple, el factorial de 4 és 4!=4

·

3

·

2

·

1=24. En el nostre plànol, per anar de A a B hem de fer 3 moviments horitzontals i 2 de verticals. Sumem els moviments verticals i horitzontals i fem el factorial del número que surt 3+2=5 i 5!=5

·

4

·

3

·

2

·

1=120, fem els factorials del nombre de camins verticals i horitzontals 3!=3

·

2

·

1=6 i 2!=2

·

1=2. Multipliquem aquests dos últims factorials 6

·

2=12 i finalment fem la divisió 120/12=10. Per tant hi ha 10 camins diferents per anar des del punt A al punt B. Us podeu entretenir a dibuixar-los.