Què és el principi de Kruskal?

Avui us proposo un joc. A continuació us reprodueixo un fragment del sonet Lo campanar de Lleida de Magí Morera:

com miranda els bells termes lleidatans,

s’enlaira un campanar fet per gegants

o per homes de raça gegantina. 

Quan guaita cap avall, l’aigua veïna

del riu li dona espill i l’horta encants;

i guaitant cap amunt, toca amb les mans

i conversa amb la lluna i la boirina.

Preneu una paraula a l’atzar del text, per exemple “muntanya” que té 8 lletres, i ara compteu 8 paraules a partir de “muntanya”, aneu a parar a “lleidatans”, que té 10 lletres. Compteu 10 paraules a partir de “lleidatans” i arribareu a “homes” que té 5 lletres (vigileu que “s’enlaira” són dos paraules). Torneu a comptar 5 paraules i aneu a “guaita” que té 6 lletres, compteu 6 paraules més i arribareu a “del” que té 3 lletres. Compteu 3 paraules fins a “dona” que té 4 lletres, compteu 4 paraules fins a “horta” que té 5 lletres, compteu 5 paraules fins “amunt” de 5 lletres, torneu a comptar 5 paraules fins a “i” que té 1 lletra, per tant arribeu a “conversa” que té 8 lletres i ja no podeu comptar més perquè se’ns acaba el text.

Si repetiu el mateix procés començant amb una altra paraula, per exemple amb “domina” ens portarà fins la paraula “lleidatans” i com aquesta paraula ja ha sortit en l’exemple anterior acabarem el procediment a “conversa”. Si comenceu el joc amb “miranda” seguireu amb “un”, “fet”, “o”, “per”, “raça”, “cap”. “aigua”, “dona”, “horta”, “amunt”, “i” i acabareu a “conversa” com en els dos casos anteriors. I si comenceu el procediment des de la paraula “bells” veureu que també acabareu a “conversa”.

És a dir, començant el joc amb totes les paraules que hem provat sempre acabem a la paraula “conversa”. El truc està en el fet que quan dos successions de paraules arriben a la mateixa paraula a partir d’aquella ja coincideixen fins acabar en una mateixa paraula. Però això passarà sempre amb totes les paraules? En principi no, però la probabilitat de trobar una paraula inicial en un text que en començar per aquesta paraula no arribem a la mateixa paraula final tendeix a zero com més llarg és el text. És a dir, com més paraules té un text més complicat és trobar una paraula a partir de la qual ens falli el joc.

El primer que s’adonà d’això fou el matemàtic i físic nord-americà Martin Kruskal (1925-2006) i d’aquí el nom de principi de Kruskal a aquesta teoria. Tanmateix qui la va popularitzar va ser el divulgador Martin Gardner (1914-2010) en la seva columna Mathematical Games de la revista Scientific American l’any 1978.El principi de Kruskal també es pot aplicar a una baralla de cartes fent servir el número de la carta per a comptar. És a dir, s’estenen totes les cartes d’una baralla cap per avall sobre una taula, es comença per una carta a l’atzar, es gira, es compta a partir del número de la carta i així successivament. La probabilitat que sempre s’arribi a la mateixa carta al final del procés és del 83%. De fet, com més baixos siguin els números de les primeres cartes més efectivitat té el joc. Un bon truc de màgia per a fer als amics endevinant la carta que sortirà al final.

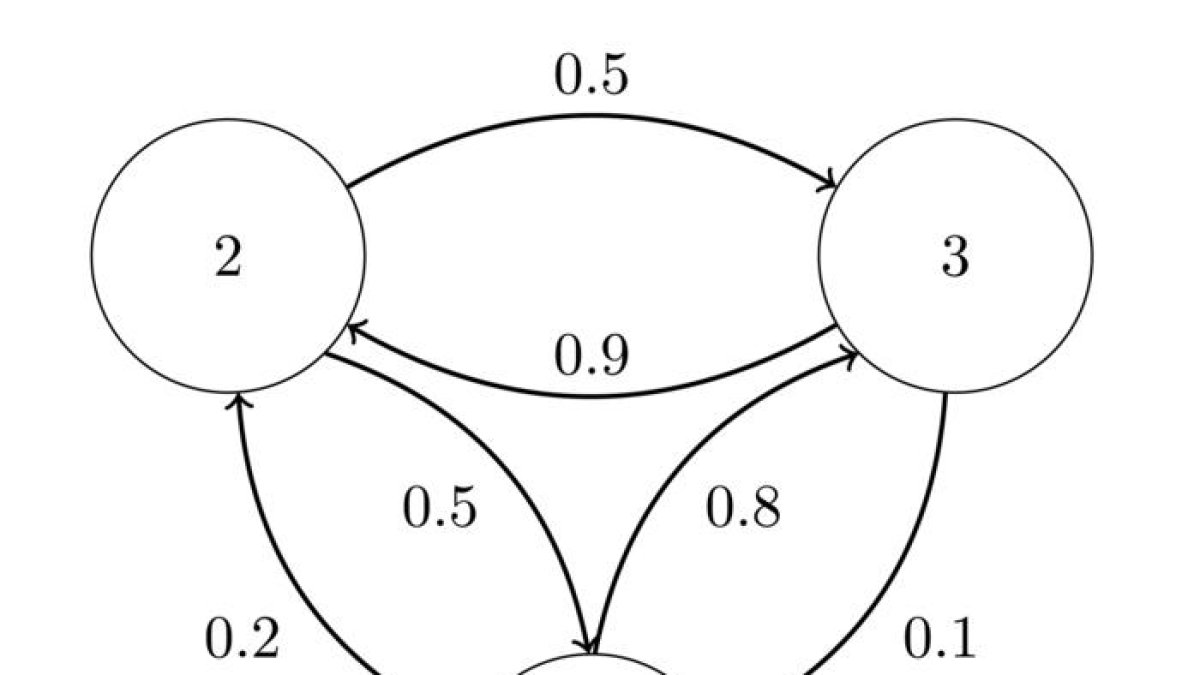
Cadenes de Markov Aquest algoritme es pot modelitzar mitjançant el que s’anomenen cadenes de Markov. Les cadenes de Markov són processos que s’apliquen quan existeix una successió d’esdeveniments en els quals la probabilitat que en succeeixi algun depèn només de la probabilitat que succeeixi l’anterior. S’utilitzen per a fer previsions en finances, meteorologia, votacions, salut...